Radionuclide Decay Chain

Radioactivity refers to the amount of ionizing radiation released by a material. Whether it emits alpha or beta particles, gamma rays, x-rays, or neutrons, a quantity of radioactive material is expressed in terms of its radioactivity (or simply its activity). This represents how many atoms in the material decay in a given time period. The units of measurement for radioactivity are the curie (roughly the activity of one gram of Radium-226) and becquerel (amount of a radioactive material that will undergo one transformation per second). The U.S. unit is the Curie (Ci) and the international unit is the Becquerel (Bq).
Source: (https://www.epa.gov/radiation/radiation-basics#tab-3)

Radioactive decay is the emission of energy in the form of ionizing radiation. When it decays, a radionuclide transforms into a different atom - a decay product. The atoms continuously transform into new decay products until they reach a stable state and are no longer radioactive. The series of decay products created to reach this balance is called the decay chain.
Source: (https://www.epa.gov/radiation/radioactive-decay)

As a radionuclide decays over time, the activity, or amount of ionizing radiation released, can be quantified for the entire chain if the starting amount of activity for the parent is known. For simple decay chains (one-to-one decay, no branching fractions), this calculation is straight-forward using the derivatives of Lamba, the decay constant. For more complex chains where many daughters are formed with multiple branches, this calculation becomes much more difficult requiring simultaneous equations of derivatives of Lambda and branching fractions.

This tool can predict the activity after a period of time (T) given a measurement of activity (A) for the chain parent. Graphs are provided to show the simultaneous decay rates and ingrowth, as well as tabular output at time-point T and all the decay half-life intervals. The activities can then be used to compare to Priminary Remediation Goals (PRGs) for a particular scenario, a composite PRG (Figure 1), and calculate risk or dose.

Figure 1. f_i is the fractional activity of the radionuclide. This value is 1 for the parent nuclide and the progeny:parent activity ratio for all other nuclides.

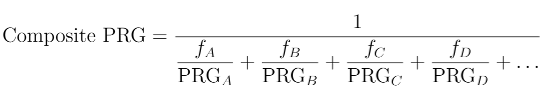
The activities of chain members are solved by a hybrid forward-euler differential equation algorithm published by Leggett et al.² This numerical integration method was used in conjunction with the ICRP 107 decay database, where the progeny, branching ratios, and half-lives for each radionuclide (excluding stable isotopes) are specified .

The system of linear differential equations is defined by the following equation:

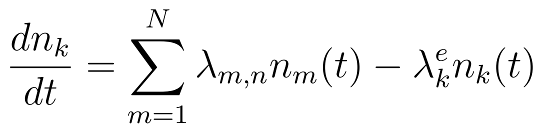
Where:

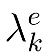	is the effective decay constant,
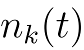	is the number of atoms of the kth member of the chain, and
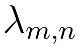	is the partial decay constant from the mth to the nth nuclide in the decay series.

Mathematically the solver then utilizes the following:

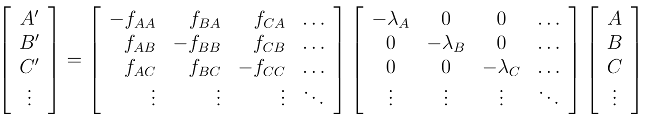
The Bateman series is a set of linear, first order differential equations. However, while the solution can be written explicitly for short chains with little effort (Figure 2 below), the closed form solution is unwieldy for longer chains. It represents the abundances and activities of radionuclides in a decay chain as a function of time. In some chains computational errors arise due to numerical instabilities associated with pairs of similar decay constants. For this reason, numerical integration is often a more practical approach for estimating chain member activities.

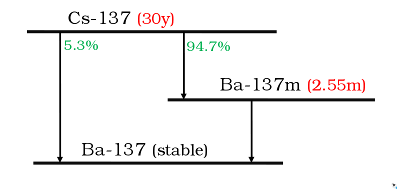
Figure 2. Radionuclide chain decay scheme of Cs-137 showing its half-life (t_1/2) values in red and branching fractions in green.

Fields that are highlighted are required.